I.45

To construct, in a given rectilineal angle, a parallelogram equal to a given rectilineal figure.

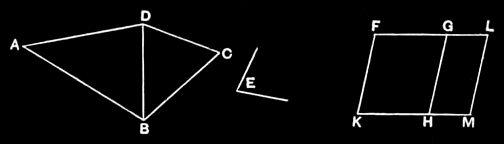
Let ABCD be the given rectilineal figure and E the given rectilineal angle; thus it is required to construct, in the given angle E, a parallelogram equal to the rectilineal figure ABCD.

Let DB be joined, and let the parallelogram FH be constructed equal to the triangle ABD, in the angle HKF which is equal to E; [I.42] let the parallelogram GM equal to the triangle DBC be applied to the straight line GH, in the angle GHM which is equal to E. [I.44]

Then, since the angle E is equal to each of the angles HKF, GHM, the angle HKF is also equal to the angle GHM. [I.cn.1]

Let the angle KHG be added to each; therefore the angles FKH, KHG are equal to the angles KHG, GHM.

But the angles FKH, KHG are equal to two right angles; [I.29] therefore the angles KHG, GHM are also equal to two right angles.

Thus, with a straight line GH, and at the point H on it, two straight lines KH, HM not lying on the same side make the adjacent angles equal to two right angles; therefore KH is in a straight line with HM. [I.14]

And, since the straight line HG falls upon the parallels KM, FG, the alternate angles MHG, HGF are equal to one another. [I.29]

Let the angle HGL be added to each; therefore the angles MHG, HGL are equal to the angles HGF, HGL. [I.cn.2]

But the angles MHG, HGL are equal to two right angles; [I.29] therefore the angles HGF, HGL are also equal to two right angles. [I.cn.1] Therefore FG is in a straight line with GL. [I.14]

And, since FK is equal and parallel to HG, [I.34] and HG to ML also,

KF is also equal and parallel to ML; [I.cn.1;:ref:I.30 <I.30>] and the straight lines KM, FL join them (at their extremities); therefore KM, FL are also equal and parallel. [I.33] Therefore KFLM is a parallelogram.

And, since the triangle ABD is equal to the parallelogram FH, and DBC to GM,

the whole rectilineal figure ABCD is equal to the whole parallelogram KFLM.

Therefore the parallelogram KFLM has been constructed equal to the given rectilineal figure ABCD, in the angle FKM which is equal to the given angle E.

Q. E. D.

Note

2, 3, 6, 45, 48. rectilineal figure, in the Greek

rectilineal

simply, without figure,

εὐθύγραμμον being here used as a substantive, like the similarly formed παραλληλόγραμμον.