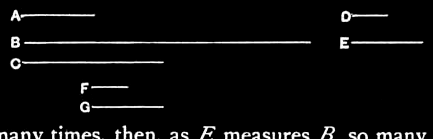
VIII.20

If one mean proportional number fall between two numbers, the numbers will be similar plane numbers.

For let one mean proportional number C fall between the two numbers A, B; I say that A, B are similar plane numbers.

Let D, E, the least numbers of those which have the same ratio with A, C, be taken; [VII.33] therefore D measures A the same number of times that E measures C. [VII.20]

Now, as many times as D measures A, so many units let there be in F; therefore F by multiplying D has made A, so that A is plane, and D, F are its sides.

Again, since D, E are the least of the numbers which have the same ratio with C, B, therefore D measures C the same number of times that E measures B. [VII.20]

As many times, then, as E measures B, so many units let there be in G; therefore E measures B according to the units in G; therefore G by multiplying E has made B.

Therefore B is plane, and E, G are its sides.

Therefore A, B are plane numbers.

I say next that they are also similar.

For, <*> since F by multiplying D has made A, and by multiplying E has made C, therefore, as D is to E, so is A to C, that is, C to B. [VII.17]

Again, <*> since E by multiplying F, G has made C, B respectively, therefore, as F is to G, so is C to B. [VII.17]

But, as C is to B, so is D to E; therefore also, as D is to E, so is F to G.

And alternately, as D is to F, so is E to G. [VII.13]

Therefore A, B are similar plane numbers; for their sides are proportional. Q. E. D. 25. For, since F……27. C to B. The text has clearly suffered corruption here. It is not necessary to infer from other facts that, as D is to E, so is A to C; for this is part of the hypotheses (ll. 6, 7). Again, there is no explanation of the statement (l. 25) that F by multiplying E has made C. It is the statement and explanation of this latter fact which are alone wanted; after which the proof proceeds as in l. 28. We might therefore substitute for ll. 25-28 the following. “For, since E measures C the same number of times that D measures A [l. 8], that is, according to the units in F [l. 10], therefore F by multiplying E has made C. And, since E by multiplying F, G,” etc. etc.