Book IV¶
Construction of Rectilinear Figures In and Around Circles¶
Inscription and circumscription of triangles and of regular polygons in and about circles
Definitions¶
IV.def.1
A rectilineal figure is said to be inscribed in a rectilineal figure when the respective angles of the inscribed figure lie on the respective sides of that in which it is inscribed.
IV.def.2
Similarly a figure is said to be circumscribed about a figure when the respective sides of the circumscribed figure pass through the respective angles of that about which it is circumscribed.
IV.def.3
A rectilineal figure is said to be inscribed in a circle when each angle of the inscribed figure lies on the circumference of the circle.
IV.def.4
A rectilineal figure is said to be circumscribed about a circle, when each side of the circumscribed figure touches the circumference of the circle.
IV.def.5
Similarly a circle is said to be inscribed in a figure when the circumference of the circle touches each side of the figure in which it is inscribed.
IV.def.6
A circle is said to be circumscribed about a figure when the circumference of the circle passes through each angle of the figure about which it is circumscribed.
IV.def.7
A straight line is said to be fitted into a circle when its extremities are on the circumference of the circle.
Propositions¶
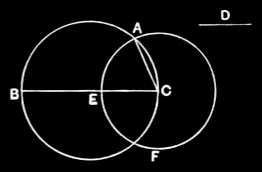
IV.1
Into a given circle to fit a straight line equal to a given straight line which is not greater than the diameter of the circle.
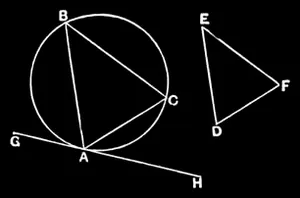
IV.2
In a given circle to inscribe a triangle equiangular with a given triangle.
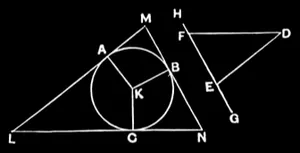
IV.3
About a given circle to circumscribe a triangle equiangular with a given triangle.
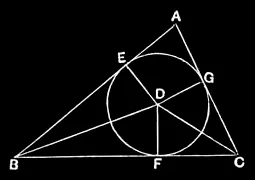
IV.4
In a given triangle to inscribe a circle.
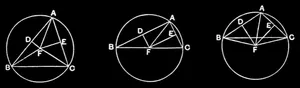
IV.5
About a given triangle to circumscribe a circle.
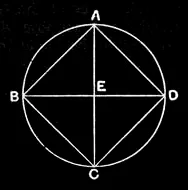
IV.6
In a given circle to inscribe a square.
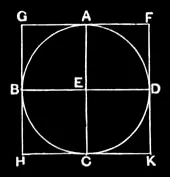
IV.7
About a given circle to circumscribe a square.
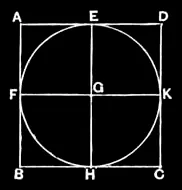
IV.8
In a given square to inscribe a circle.
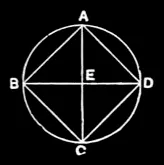
IV.9
About a given square to circumscribe a circle.
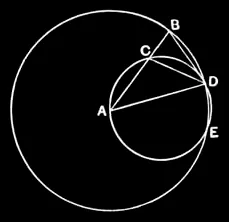
IV.10
To construct an isosceles triangle having each of the angles at the base double of the remaining one.
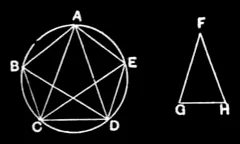
IV.11
In a given circle to inscribe an equilateral and equiangular pentagon.
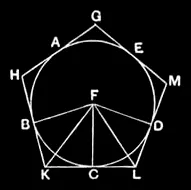
IV.12
About a given circle to circumscribe an equilateral and equiangular pentagon.
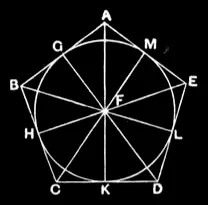
IV.13
In a given pentagon, which is equilateral and equiangular, to inscribe a circle.
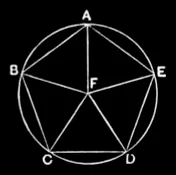
IV.14
About a given pentagon, which is equilateral and equiangular, to circumscribe a circle.
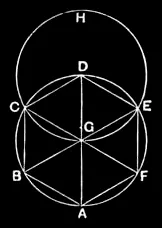
IV.15
In a given circle to inscribe an equilateral and equiangular hexagon.
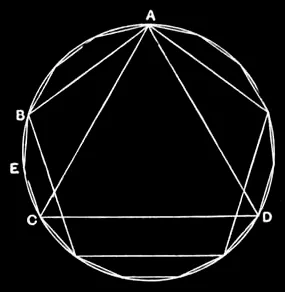
IV.16
In a given circle to inscribe a fifteen-angled figure which shall be both equilateral and equiangular.
