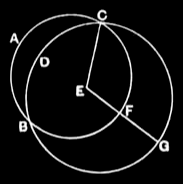
III.5¶
If two circles cut one another, they will not have the same centre.
For let the circles ABC, CDG cut one another at the points B, C; I say that they will not have the same centre.
For, if possible, let it be E; let EC be joined, and let EFG be drawn through at random.
Then, since the point E is the centre of the circle ABC,
EC is equal to EF. [I.def.15]
Again, since the point E is the centre of the circle CDG,
EC is equal to EG.
But EC was proved equal to EF also;
therefore EF is also equal to EG, the less to the greater : which is impossible.
Therefore the point E is not the centre of the circles ABC, CDG.
Therefore etc. Q. E. D.
