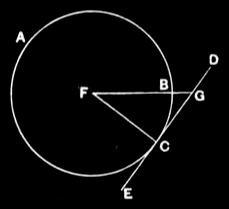
III.18¶
If a straight line touch a circle, and a straight line be joined from the centre to the point of contact, the straight line so joined will be perpendicular to the tangent.
For let a straight line DE touch the circle ABC at the point C, let the centre F of the circle ABC be taken, and let FC be joined from F to C; I say that FC is perpendicular to DE.
For, if not, let FG be drawn from F perpendicular to DE.
Then, since the angle FGC is right,
the angle FCG is acute; [I.17]
and the greater angle is subtended by the greater side; [I.19]
therefore FC is greater than FG.
But FC is equal to FB;
therefore FB is also greater than FG, the less than the greater: which is impossible.
Therefore FG is not perpendicular to DE.
Similarly we can prove that neither is any other straight line except FC;
therefore FC is perpendicular to DE.
Therefore etc. Q. E. D. the tangent, ἡ ἐφαπτομένη.
