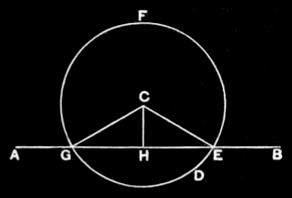
I.12

To a given infinite straight line, from a given point which is not on it, to draw a perpendicular straight line.

Let AB be the given infinite straight line, and C the given point which is not on it; thus it is required to draw to the given infinite straight line AB, from the given point C which is not on it, a perpendicular straight line.

For let a point D be taken at random on the other side of the straight line AB, and with centre C and distance CD let the circle EFG be described; [I.post.3]

let the straight line EG

be bisected at H, [I.10] and let the straight lines CG, CH, CE be joined. [I.post.1]

I say that CH has been drawn perpendicular to the given infinite straight line AB from the given point C which is not on it.

For, since GH is equal to HE, and HC is common, the two sides GH, HC are equal to the two sides EH, HC respectively; and the base CG is equal to the base CE; therefore the angle CHG is equal to the angle EHC. [I.8] And they are adjacent angles.

But, when a straight line set up on a straight line makes the adjacent angles equal to one another, each of the equal angles is right, and the straight line standing on the other is called a perpendicular to that on which it stands. [I.def.10]

Therefore CH has been drawn perpendicular to the given infinite straight line AB from the given point C which is not on it.

Q. E. D.

Note

2. a perpendicular straight line

, κάθετον εὐθεῖαν γραμμἡν. This is the full expression for a perpendicular, κάθετος meaning let fall or let down, so that the expression corresponds to our plumb-line. ἡ κάθετος is however constantly used alone for a perpendicular, γραμμἡ being understood.

Note

10. on the other side of the straight line AB

, literally towards the other parts of the straight line AB,

ἐπὶ τὰ ἕτερα μέρη τῆς AB. Cf. on the same side

(ἐπὶ τὰ αὐτὰ μέρη) in I.post.5 and in both directions

(ἐφ̓ ἑκάτερα τὰ μἑρη) in I.def.23.