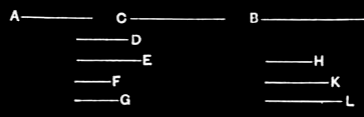
X.12¶
Magnitudes commensurable with the same magnitude are commensurable with one another also.
For let each of the magnitudes A, B be commensurable with C; I say that A is also commensurable with B.
For, since A is commensurable with C, therefore A has to C the ratio which a number has to a number. [X.5]
Let it have the ratio which D has to E.
Again, since C is commensurable with B, therefore C has to B the ratio which a number has to a number. [X.5]
Let it have the ratio which F has to G.
And, given any number of ratios we please, namely the ratio which D has to E and that which F has to G, let the numbers H, K, L be taken continuously in the given ratios; [cf. VIII.4] so that, as D is to E, so is H to K,
and, as F is to G, so is K to L.
Since, then, as A is to C, so is D to E, while, as D is to E, so is H to K, therefore also, as A is to C, so is H to K. [V.11]
Again, since, as C is to B, so is F to G, while, as F is to G, so is K to L, therefore also, as C is to B, so is K to L. [V.11]
But also, as A is to C, so is H to K; therefore, ex aequali, as A is to B, so is H to L. [V.22]
Therefore A has to B the ratio which a number has to a number; therefore A is commensurable with B. [X.6]
Therefore etc. Q. E. D.
